Math 3; Distorted Ovals

DISTORED OVALS
A recent math issue I tried to tackle is the next thing....
We know what we get if we take a board drive a nail into it take a string and a pencil and move the pen around in such a way that a circle is obtained.
and we know the formula of a circle as well; (for the technique see the picture above).
R^2 = SQRT[ (x-a)^2 + (y-b)^2 ]
We also know what we get if we drive 2 nails into a board and repeat the same practice. We get an oval. We also know the formula even of these ovals which are easy to find on the internet.

The question rises then what happens if we move beyond that. That is if we drive in 3 , 4, 5 etc nails into a board at random and put a string around that and draw the figure of that.
Now this approach is different than what is known as Cartesian Ovals and also no what is known as Cassini ovals.
This distorted oval is totaly new, As far as I know.
Well I, thank God, have done so and these are some results of that right below is a 3 point P1, P2 and P3 "distorted oval"
Below that is a 5 point distorted oval.


Another question rises if one of these points in a regular oval would not ba a point but rather a circle around which the cord moves.
Well this next picture shows us what you would get in that case:

As you can see that is a real egg shape in more or lesser extend. A real egg-oval or oval-egg
In doing this "research" I had to draw some extra lines for myself to get things calulated and more numerical which you can see at the numbers I have written along with it.
But now it gets a bit harder to derive the formulas to destrcibe these figures. But I was able to work it out. but let me tell you it is a teadious job. to get it done.
I have worked out the 5 point distorted oval.
and since there are 5 different points, All coordinates are in cm, but the same would go for any type of unit like inch, mm, miles, etc
P0 = (x, y) = (0 , 0) which is the mathematical centre so to speak
P1 = (8 , 5)
P2 = (12 , 0)
P3 = (3 , -3)
P4 = (-2, -3)
And the pen is located in position Ppen (Xpen, Ypen)
To make it easier on ourselves for all distances of the point Pi I will precalculate them right here and round them of on 2 decimals since the measurements are not more accurate than that.
P0 - P1 = SQRT( (0-8)^2 + (0-5)^2 ) = 9.43 cm
P1 - P2 = SQRT( (8-12)^2 + (5-0)^2 ) = 6.40 cm
P2 - P3 = SQRT( (12-3)^2 + (0-(-3))^2 ) = 9.50 cm
P3 - P4 = SQRT( ((-2)-3)^2 + ((-3)- (-3) )^2 ) = 5,00 cm
P4 - P0 = SQRT( (0 - (-2))^2 + (0 - (-3) )^2 ) = 3,60 cm
As you can right away see I had to devide the 5 point based Distorted Oval (D.O.) in 10 different sections, and if you would do the same exersize then you would find out you have to. This is because the cord (which I took to be about 36 cm in circumference) will move in such a way that there are intermediate sections that determine the shape of the D.O. in that area.
And it turns out that 5 points will lead to 10 different sections that mathematically need to be treated seperately. Also it was found that there are 2 different basic type of sections: 1 type of sections where all the points are touched by the cord and 1 type of section where only 4 of the 5 points are touched. Both type of sections must be treated mathematically different.
And as you can see in the picture I drew the both sections with different type of lines: (- - - - - -) for one of the sections with 4 touching points
and (VVVVVVVVVVVVV) for the 5 touching point section.
Since there are 10 sections we have 5 of sections of each type. Also the formula for these section types are the same all be-it different for the different sections.
For the first S1 in which the pen is P4 to Ppen to P1:
The formula's are:
|P1, P2| + |P2, P3| + |P3, P4| + |P4,Ppen| + |Ppen, P1| = circumference of the cord = 36
this is
|P1, P2| + |P2, P3| + |P3, P4| + SQRT( (-2 - Xpen)^2 + (-3 -Ypen)^2 ) + SQRT (( Xpen - 8)^2 + (Ypen - 5)^2)
Which gives:
6.40 + 9.50 + 5.00 + SQRT( (-2 - Xpen)^2 + (-3 -Ypen)^2 ) + SQRT (( Xpen - 8)^2 + (Ypen - 5)^2) = total circumference of the cord = 36
For the second section S2 the formula is slightly different since the cord is touching all the points P0, P1 P2 P3 and P4 via Ppen.
Ppen is, in section S2 between P0 and P1.
So the total formula becomes:
|P0, Ppen| + |Ppen, P1| + |P1, P2| + |P2, P3| + |P3, P4| + |P4, P0| =
SQRT( (-2 - Xpen)^2 + (-3 -Ypen)^2 ) + SQRT (( Xpen - 8)^2 + (Ypen - 5)^2)
SQRT( 0-Xpen)^2 + (0-Ypen)^2) + SQRT(Xpen - 8)^2 + (Ypen - 5)^2) + 6.40 + 9.50 + 5.00 + 3.60
This procedure was repeated and I did that a long while ago on paper and took pictures of that:

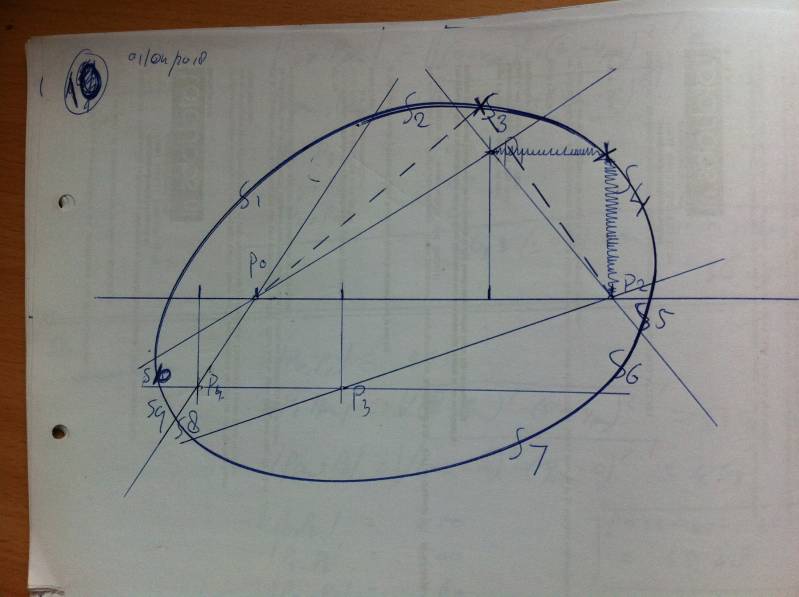







all these numbers are gained by measuring: and the measurements give us an measurment for the circumference of
(36.3 + 36.25 + 36.05 + 35.48 + 36.13 + 36.33 + 36.13 + 35.98 + 35.83 +36.03) / 10 = 36,051 cm
Now one can ask does this all have a practical application; well it might have if one thinks of irregular orbits of smaller objects around some heavy objects (that some how seem to have been stablized with respect to each other even if it is temporarily. or machinery that needs not an entire perfect oval but some how slight;y distorted. Or irregular stones that have been formed by water running passed them. things like that.
Maak jouw eigen website met JouwWeb